Adverserial Attack - Fool the Cat Grass Classifier Using Carlini and Wagner Attack

08 Nov 2019 in Classifier

This project based on the cat-grass classifier developed using the Gaussian linear model. This project exploits possible vulnerabilities in the linear classifier, which can also apply to the deep neural network, and can be attacked easily if the parameters are known. At the end we are able to input a perturbed image that is visually identical to the input image but the output result is mostly grass.

This project based on the cat-grass classifier developed using the Gaussian linear model. This project exploits possible vulnerabilities in the linear classifier, which can also apply to the deep neural network, and can be attacked easily if the parameters are known. The attack used here will be Carlini and Wagner Attack (CW Attack) developed by Nicholas Carlini and David Wagner (original paper can be found here). At the end we are able to input a perturbed image that is visually identical to the input image but the output result is mostly grass.

This project and all associated data are provided by Prof. Stanley Chan from Purdue University for learning purposes only.

Part 1 - Setting Up

This project is based on Building a Linear Gaussian Classifier to Classify Cat and Grass. If you have not seen this project, please take a look and be familier with the project. The adversarial attack is performed on the classifier built by that project.

The programming environment setup for this project is same as Building a Linear Gaussian Classifier to Classify Cat and Grass.

Part 2 - Theory

Part 2.1 - Problem

The problem of vulnerabilities of the neural network was brought to attention by Ian Goodfellow et al. in 2015 by the paper Explaining and Harnessing Adversarial Examples. The basic idea is that the neural network can be fooled by perturbing the input as an example shown in Figure 1.

Fig.1 - Adversarial example of fooling a classifier with an input plus noise. Image provided by the Ian Goodfellow et al.

Adversarial attack is defined as: Let $\pmb{x}_0\in\mathbb{R}^d$ be a data point belong to class $\mathcal{C}_i$. Define a target class $\mathcal{C}_t$. An adversarial attack is a mappint $\mathcal{A}:\mathbb{R}^d\rightarrow\mathbb{R}^d$ such that the perturbed data $\pmb{x}=\mathcal{A}\left(\pmb{x}_0\right)$ is misclassified as $\mathcal{C}_t$. In some situation, the target class may not be defined and the attack work as trying to misclassify to any of the other classes.

There are two types of attack: white-box attack and black-box attack. In a white-box attack, the attacker knows everything about the model - the structure, weights, etc. The attack can be structured to fool the model easily based on the gradient of the model. The black-box attack is treating the model as a black box and tries to fool it. This is much harder since the gradient is unknown and, in practice, the attacker can only probe the model/classifier finite times. In the real world, most of the situations are similar to the black-box where the model is unknown to the public.

There are three main forms of attack: minimum norm attack, maximum allowable attack, and regularization-based attack. We will give a brief explanation of all of those but the project only uses the CW attack, which is a form of regularization-based attack. If you are uninterested in other forms of attack and only interested in this project, you are free to skip Part 2.2, 2.3 and 2.5.

Part 2.2 - Minimum Norm Attack

The idea of the minimum norm attack is to perturb the input image as less as possible for it to land on the target class (or any other class). The quantity of perturbation is defined by some mathematical metrics such as $l_2$ distance. The mathematical definition is:

$$\min_{\pmb{x}}\|\pmb{x}-\pmb{x}_0\|\\\text{subject to\ \ \ }\max_{j\neq t}\{g_j(\pmb{x})\}-g_t(\pmb{x})\leq 0$$

where $g_k(\pmb{x})$ is the output for class k (kind of like the score for class k, higher means more likely). The equation can be interpreted as we are trying to minimize the norm ($L1$, $l_2$, or other norms) between the perturbed image and the input image while keeping the classifier output highest score for the target class $\mathcal{C}_t$.

We can make observations here. Firstly, we do not need to solve the inequality - solving for equality is enough. When they are equal, we are at the decision boundary between two classes, and we can simply add a small step $\epsilon$ towards the target class. Secondly, the attack does not have to be optimal - being suboptimal is fine. The goal is to have the classifier/model misclassify on the input, and the optimal solution would be picking the attack with the least perturbation. However, attack with more perturbation than the optimal solution along the same direction works just fine. It is still possible to fool a classifier with a less nasty attack.

The DeepFool Attack proposed by Moosavi-Dezfooli et al. in 2016 is based on this formulation as trying to solve the optimization:

$$\min_{\pmb{x}}\|\pmb{x}-\pmb{x}_0\|\\\text{subject to\ \ }g(\pmb{x})=0$$

where $g(\pmb{x})=0$ is the nonlinear decision boundary separating the two classes.

Appendix 1 provides an example for 2 class linear classifier attack detailed math solution and Appendix 2 shows the derivation for iterative DeepFool Attack solution based on first-order approximation.

Part 2.3 - Maximum Allowable Attack

Maximum allowable attack is, instead of forcing the classifier to land on a different class and minimizing the norm like the minimum-norm attack does, fixing the amount of perturbation can be added with the goal of maximizing the the score for the target class. Mathematically defined as:

$$\min_{\pmb{x}}\max_{j\neq t}\{g_j(\pmb{x})\}-g_t(\pmb{x})\\\text{subject to\ \ \ }\|\pmb{x}-\pmb{x}_0\|\leq\eta$$

where $\eta$ is the maximum allowable attack strength.

The fast gradient sign method (FGSM) proposed by Goodfellow et al. is 2014 is based on the formulation as trying to solve

$$\max_{\pmb{x}}J(\pmb{x},\pmb{w})\\\text{subject to\ \ \ }\|\pmb{x}-\pmb{x}_0\|_{\infty}\leq\eta$$

where

$$J(\pmb{x},\pmb{w})=g_t(\pmb{x})-\max_{i\neq t}\{g_{i}(\pmb{x})\}.$$

The function $J(\pmb{x},\pmb{w})$ can be seen as the score function for class t. The goal of training is trying to find a good $\pmb{w}$ for minimizing $J(\pmb{x},\pmb{w})$ (minimize the score for incorrect class) and the goal of attack is to find a nasty $\pmb{x}$ for maximizing $J(\pmb{x},\pmb{w})$.

Appendix 3 shows a detailed solution for two class maximum allowable attack and Appendix 4 extends it to FGSM and i-FGSM (iterative fast gradient sign method).

Part 2.4 - Regularized Attack

Different from the minimum-norm attack and the maximum allowable attack where explicit constraints are explicitly placed into the optimization problem, the regularized attack adds a regularization term to the objective function instead of placing a hard constraint. Mathematically, it is trying to solve

$$\min_{\pmb{x}}\|\pmb{x}-\pmb{x}_0\|^2+\lambda\left(\max_{j\neq t}\{g_{j}(\pmb{x})\}-g_{t}(\pmb{x})\right).$$

With a two class example, we can simplify the problem to

$$\min_{\pmb{x}}\frac{1}{2}\|\pmb{x}-\pmb{x}_0\|^2+\lambda\left(\pmb{w}^T\pmb{x}+w_0\right)$$

where $\pmb{w}^T\pmb{x}+w_0$ is the decision boundary between the two classes and adding a factor to the first term does not change the optimality of the final solution.

We can easily solve for optimal $\pmb{x}$ when $l_2$ norm is used:

$$\begin{aligned}\varphi(\pmb{x})&=\frac{1}{2}\|\pmb{x}-\pmb{x}_0\|^2+\lambda\left(\pmb{w}^T\pmb{x}+w_0\right)\\0=\nabla\varphi(\pmb{x})&=(\pmb{x}-\pmb{x}_0)+\lambda\pmb{w}\\\pmb{x}&=\pmb{x}_0-\lambda\pmb{w}\end{aligned}$$

The Carlini and Wagner Attack (C&W Attach) is based on this formulation. It is defined as:

$$\min_{\pmb{x}}\|\pmb{x}-\pmb{x}_0\|^2+\lambda\cdot\max\left\{\left(\max_{j\neq t}\{g_{j}(\pmb{x})\}-g_{t}(\pmb{x})\right),0\right\}.$$

If $\max_{j\neq t}\{g_{j}(\pmb{x})\}-g_{t}(\pmb{x})<0$, then the class is already misclassified and no action is needed. If $\max_{j\neq t}\{g_{j}(\pmb{x})\}-g_{t}(\pmb{x})>0$, then the regularization term will have an effect on the problem which will cause perturbation to the input. Let’s define the rectifier function as:

$$\xi(x)=\max(x,0)$$

and simplify the objective function to

$$\min_{\pmb{x}}\|\pmb{x}-\pmb{x}_0\|^2+\lambda\cdot\xi\left(\max_{j\neq t}\{g_{j}(\pmb{x})\}-g_{t}(\pmb{x})\right).$$

One way to think about this is to see the regularized attack as a soft-version of the minimum-norm attack:

$$\begin{aligned}\min_{\pmb{x}}\|\pmb{x}-\pmb{x}_0\|+\iota(\pmb{x})\\\iota(\pmb{x})=\begin{cases}0,&\text{if } \max_{j\neq t}\{g_{j}(\pmb{x})\}-g_{t}(\pmb{x})<0\\+\infty,&\text{othersise.}\end{cases}\end{aligned}$$

In order to solve the optimization problem, we have find the gradient of $\xi$:

$$\frac{d}{dx}\xi(s)=\mathbb{I}\{s>0\}=\begin{cases}1,&\text{if } s>0,\\0,&\text{otherwise.}\end{cases}$$

where $\mathbb{I}$ is usually noted as the indicator variable. Let $i^*=\text{arg}\max_{j\neq t}\{g_j(\pmb{x})\}$, now we can find the full gradient of $\xi$:

$$\begin{aligned}&\nabla_{\pmb{x}}\ \xi\left(\max_{j\neq t}\{g_j(\pmb{x})\}-g_t(\pmb{x})\right)\\=&\nabla_{\pmb{x}}\ \xi\left(g_{i^*}(\pmb{x})-g_t(\pmb{x})\right)\\=&\begin{cases}\nabla_{\pmb{x}}\ g_{i^*}(\pmb{x})-\nabla_{\pmb{x}}\ g_{t}(\pmb{x}),&\text{if } g_{i^*}(\pmb{x})-g_t(\pmb{x})>0,\\0,&\text{otherwise.}\end{cases}\\=&\mathbb{I}\{g_{i^*}(\pmb{x})-g_t(\pmb{x})>0\}\cdot\left(\nabla_{\pmb{x}}\ g_{i^*}(\pmb{x})-\nabla_{\pmb{x}}\ g_{t}(\pmb{x})\right)\end{aligned}$$

After knowling $\nabla_{\pmb{x}}\ \xi$, we can apply chain rule and solve for $\nabla\varphi(\pmb{x}, i^*)$:

$$\nabla\varphi(\pmb{x}, i^*)=2(\pmb{x}-\pmb{x}_0)+\lambda\cdot\mathbb{I}\{g_{i^*}(\pmb{x})-g_t(\pmb{x})>0\}\cdot\left(\nabla_{\pmb{x}}\ g_{i^*}(\pmb{x})-\nabla_{\pmb{x}}\ g_{t}(\pmb{x})\right)$$

So for a iterative approach, for iteration $k=1,2,\dots$

$$\begin{aligned}i^*&=\text{arg}\max_{j\neq t}\{g_j(\pmb{x}^{(k)})\}\\\pmb{x}^{(k+1)}&=\pmb{x}^{(k)}-\alpha\nabla\varphi(\pmb{x}^{(k)};i^*)\end{aligned}$$

where $\alpha$ is the gradient descent step size and $\lambda$ is the regularization parameter.

Part 2.5 - Comparing Three Methods

Guo et al. did a comparison between DeepFool, FGSM, i-FGSM, and Carlini-Wagner when developing defense methods. Following two images shows the comparison results:

Fig.1 - Amount of perturbations added based on adversary strength.

Fig.2 - The effectiveness of different defense stategies against attacks.

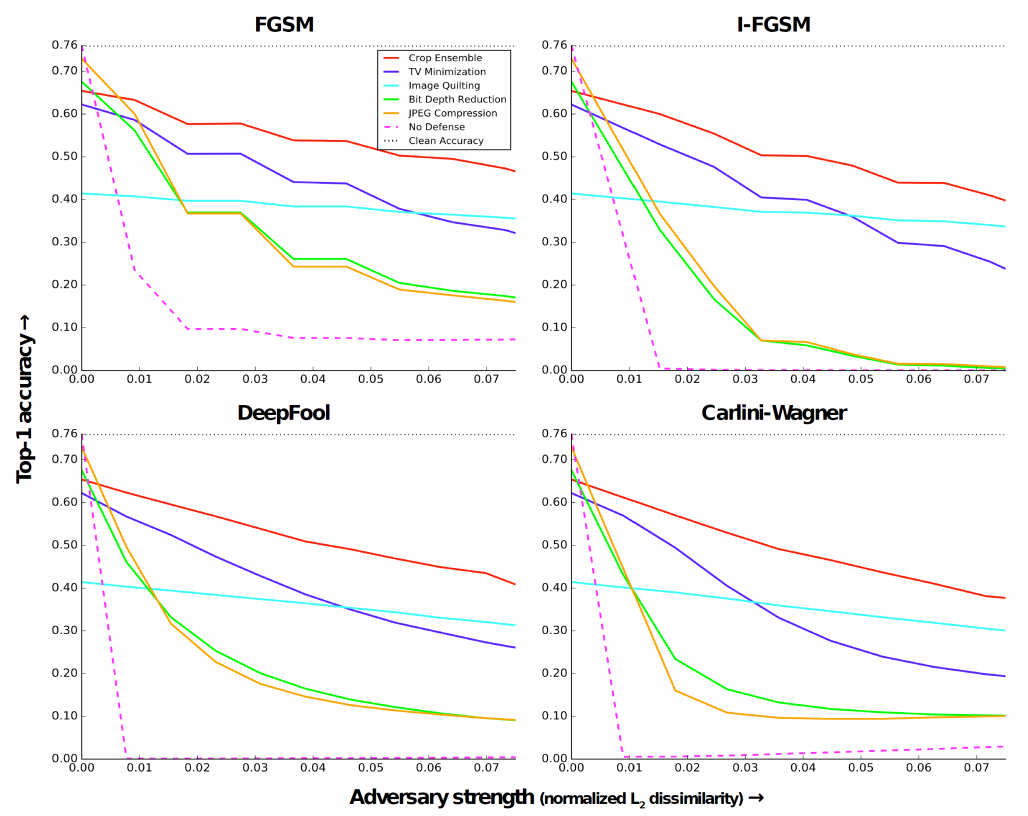
Part 3 - Attack!

The goal of this part to demostrate how to fool the classifier by making the cat patches to be classified as grass.

Part 3.1 - Equation Revision

The decision rules defined in building the linear classifier is to compare

$$f_{\pmb{Z}\vert\text{class}}(\pmb{z}\vert\text{cat})f(\text{cat})\lessgtr f_{\pmb{Z}\vert\text{class}}(\pmb{z}\vert\text{grass})f(\text{grass})$$

which is equivalent to comparing

$$f_{\pmb{Z}\vert\text{class}}(\pmb{z}\vert\text{cat})f(\text{cat})-f_{\pmb{Z}\vert\text{class}}(\pmb{z}\vert\text{grass})f(\text{grass})\lessgtr0$$

where $\pmb{z}$ is the selected patch from the image. Recall that the $\log$ of probability is:

$$\begin{aligned}&-\frac{1}{2}\left(\pmb{z}-\pmb{\mu}\right)^T\pmb{\Sigma}^{-1}\left(\pmb{z}-\pmb{\mu}\right)-\frac{d}{2}\log(2\pi)-\frac{1}{2}\log(\vert\pmb{\Sigma}\vert)+\log(f(\text{class}))\\ =&-\frac{1}{2}\left[\pmb{z}^T\pmb{\Sigma}^{-1}\pmb{z}-\pmb{\mu}^T\pmb{\Sigma}^{-1}\pmb{z}-\pmb{z}^T\pmb{\Sigma}^{-1}\pmb{\mu}+\pmb{\mu}^T\pmb{\Sigma}^{-1}\pmb{\mu}\right]-\frac{1}{2}\log(\vert\pmb{\Sigma}\vert)+\log(f(\text{class}))\\ =&-\frac{1}{2}\pmb{z}^T\pmb{\Sigma}^{-1}\pmb{z}+(\pmb{\Sigma}^{-1}\pmb{\mu})^T\pmb{x}-\frac{1}{2}\pmb{\mu}^T\pmb{\Sigma}^{-1}\pmb{\mu}-\frac{1}{2}\log(\vert\pmb{\Sigma}\vert)+\log(f(\text{class}))\end{aligned}$$

We can drop $\frac{d}{2}\log(2\pi)$ term because this is a constent same for all classes and it does not make any difference during comparision. Line 2 to line 3 is possible because the covariance matrix $\pmb{\Sigma}$ is positive semisemidefinite. Let $\pmb{W}=\pmb{\Sigma}^{-1}$, $\pmb{w}=-\pmb{\Sigma}^{-1}\pmb{\mu}$, and $w_0=\frac{1}{2}\pmb{\mu}^T\pmb{\Sigma}^{-1}\pmb{\mu}+\frac{1}{2}\log(\vert\pmb{\Sigma}\vert)-\log(f(\text{class}))$, we can simplify the equation to:

$$f_{\pmb{Z}\vert\text{class}}(\pmb{z}\vert\text{class})f(\text{class})=-\left(\frac{1}{2}\pmb{z}^T\pmb{W}\pmb{z}+\pmb{w}^T\pmb{z}+w_0\right)$$

and define the classification rule as:

$$g(\pmb{z})=\frac{1}{2}\pmb{z}^T\left(\pmb{W}_{\text{grass}}-\pmb{W}_{\text{cat}}\right)\pmb{z}+\left(\pmb{w}_{\text{grass}}-\pmb{w}_{\text{cat}}\right)^T\pmb{z}+w_{0,\text{grass}}-w_{0,\text{cat}}\\ \pmb{z}=\begin{cases}\text{cat},&\text{if } g(\pmb{z})>0\\\text{grass},&\text{otherwise}\end{cases}$$

Part 3.2 - Load Data and Calculate Variables

We will load the data from txt file into np.array same as what we did before and calculate $\pmb{W}$, $\pmb{w}$, and $w_0$. We will use $\pi_{\text{class}}$ to denote the prior of that class $f(\text{class})$.

def compute_variables(training_data, pi):
  mu = np.mean(training_data, 1)
  W = np.linalg.inv(np.cov(training_data))
  w = -np.matmul(W, mu)
  w0 = np.matmul(np.matmul(mu, W), mu) / 2 + np.log(np.linalg.det(np.cov(training_data))) / 2 - np.log(pi)

  return W, w, w0

def load_data_and_compute():
  train_grass = np.loadtxt('data/train_grass.txt', delimiter=',')
  train_cat = np.loadtxt('data/train_cat.txt', delimiter=',')
  W = [0] * 2
  w = [0] * 2
  w0 = [0] * 2
  W[0], w[0], w0[0] = compute_variables(train_grass, len(train_grass[0]) / (len(train_grass[0]) + len(train_cat[0])))
  W[1], w[1], w0[1] = compute_variables(train_cat, len(train_cat[0]) / (len(train_grass[0]) + len(train_cat[0])))

  return W, w, w0

Part 3.3 - Redefine Classifier

Since we are using $\pmb{W}$, $\pmb{w}$, and $w_0$ now, let’s redefine the classifier from previous post to use these input variables instead of the mean vector and the covariance matrix. This time we will only have the overlapping classifier and non-overlapping classifier.

def classifier_nonoverlap(img, W, w, w0):
  # find the dimension of the image
  M = len(img)
  N = len(img[0])

  output = np.zeros((M // 8 * 8, N // 8 * 8))   # initialize the output matrix
  for i in range(M // 8):
    for j in range(N // 8):
      # extract the 8x8 patch, flatten it and find the difference to the mu of cat and grass
      z = img[i * 8: i * 8 + 8, j * 8 : j * 8 + 8]
      z = z.flatten('F')

      # calculate g(x) and classify the batch based on sign(g(x))
      g = np.matmul(np.matmul(z.T, W[0] - W[1]), z) / 2 + np.matmul(z.T, w[0] - w[1]) + w0[0] - w0[1]
      if g > 0:
        output[i * 8 : i * 8 + 8, j * 8 : j * 8 + 8] = 1
  return output

def classifier_overlap(img, W, w, w0):
  # find the dimension of the image
  M = len(img)
  N = len(img[0])

  output = np.zeros((M - 8 + 1, N - 8 + 1))   # initialize the output matrix
  for i in range(M - 8 + 1):
    for j in range(N - 8 + 1):
      # extract the 8x8 patch, flatten it and find the difference to the mu of cat and grass
      z = img[i : i + 8, j : j + 8]
      z = z.flatten('F')

      # calculate g(x) and classify the pixel based on sign(g(x))
      g = np.matmul(np.matmul(z.T, W[0] - W[1]), z) / 2 + np.matmul(z.T, w[0] - w[1]) + w0[0] - w0[1]
      if g > 0:
        output[i][j] = 1
  return output

Part 3.4 - Compute Gradient of the Given Patch

The gradient using $l_2$ norm for making cat class into grass is:

$$\nabla g(\pmb{z})=\left[-2(\pmb{z}-\pmb{z}_0)-\lambda(\pmb{W}_{\text{grass}}-\pmb{W}_{\text{cat}})\pmb{z}+\pmb{w}_{\text{grass}}-\pmb{w}_{\text{cat}}\right]\cdot\mathbb{I}\{g(\pmb{z})>0\}$$

Following code snippet shows how that is achieved. We will use target_idx=0 as default to flip the cat into grass:

def gradient(z, z_0, lamb, W, w, w0, target_idx=0):
  '''
  z: 	   the current patch vector      x0: the original patch vector
  lamb:  lambda value                  W:  the Wj and Wt matrix
  w:     the wj and wt vector          w0: the w_0j and w_0t scalar
  target idx = 1 --> make cat into grass
  target idx = 0 --> make grass into cat
  '''
  j = 1 - target_idx
  t = target_idx
  # caluclate g(x) see if it is already in target class
  g = np.matmul(np.matmul(z.T, W[j] - W[t]), z) / 2 + np.matmul(z.T, w[j] - w[t]) + w0[j] - w0[t]
  if g > 0:
      return [0] * 64
  # if it is not in target class, calculate the gradient and return it
  grad = -2 * (z - z_0) - lamb * np.matmul(W[j] - W[t], z) + w[j] - w[t]
  return grad

Part 3.5 - Non-overlapping CW Attack

For non-overalpping attack, we approach is similar to what we did before: for each 8x8 patch, perturb it if necessary and clip the result into the range $[0,1]$ every iteration. We will also define a maximum number of iterations max_iter and minimum change min_change for terminating the attack. The loop will stop when either 1) the number of iterations has reached max_iter or 2) the Frobenius norm $\|\cdot\|_F$, which is the norm of the perturbation added for each iteration, is less than min_change, indicating that the attack has reached saturation. We can also save the image during attack to see how much it has changed.

def nonoverlapping_CW_attack(img, lamb, alpha, W, w, w0, save_freq=10, target_idx=0, max_iter=300, min_change=0.001):
  '''
  img:        the input image array
  lamb:       the regularization constant
  alpha:      the step size for gradient descent
  W:          the Wj and Wt matrix
  w:          the wj and wt vector
  w0:         the w_0j and w_0t scalar
  save_freq:  save image every k iteration. 0 or negative numbers mean don't save any images
  target_idx: which class to attack
  max_iter:   maximum number of iterations
  min_change: minimum change needed to prevent saturation
  '''
  idx = 0; change = 99  # initialize variables
  print(min_change)
  # M and N for the dimension of the input image
  M = len(img); N = len(img[0])

  result = np.copy(img)     # for storing the attacked image
  perturb = np.zeros((M, N))  # to keep track of the perturbation

  while idx < max_iter and change > min_change:
    for i in range(M // 8):
      for j in range(N // 8):
        # grab the current patch and the starting patch for gradient computation
        z = result[i * 8 : i * 8 + 8, j * 8 : j * 8 + 8].flatten('F')
        z_0 = img[i * 8 : i * 8 + 8, j * 8 : j * 8 + 8].flatten('F')

        # calculate the gradient
        grad = gradient(z, z_0, lamb, W, w, w0, target_idx)
        
        # add the patch to the perturbation matrix
        perturb[i * 8 : i * 8 + 8, j * 8 : j * 8 + 8] = -alpha * np.reshape(grad, (8, 8), order='F')
    
    # update the loop control variables
    idx += 1
    change = np.linalg.norm(perturb)
    # add the perturbation to the image
    result = np.clip(result + perturb, 0.0, 1.0)

    # save the image if necessary
    if save_freq > 0 and idx % save_freq == 0:
      classify_result = classifier_nonoverlap(result, W, w, w0)
      plt.imsave(f'nonoverlap_{lamb}_{idx}_img.png', result * 255, cmap='gray')
      plt.imsave(f'nonoverlap_{lamb}_{idx}_perturb.png', (result - img) * 255, cmap='gray')
      plt.imsave(f'nonoverlap_{lamb}_{idx}_clasify.png', classify_result * 255, cmap='gray')
  
  print(f'Finished in {idx} iterations.')
  return result

Part 3.6 - Overlapping CW Attack

Some changes are needed to perform the overlapping CW attack. Because the goal of keeping teh image as close to the original as possible remains, perturbing each overlapping patch can cause a huge overall perturbation to the image. In this case, we want to consider the alternative optimization problem:

$$\pmb{X}^*=\text{arg}\min_{\pmb{X}}\|\pmb{X}-\pmb{X}_0\|^2+\lambda\sum_{i=1}^{L}\max\left(g_j(\pmb{P}_i\pmb{X})-g_t(\pmb{P}_i\pmb{X}),0\right)$$

where $\pmb{X}$ is the entire image, $L$ is total number of patches and $\pmb{P}_i$ is the matrix that extracts the $i^{th}$ patch from the overall image. The gradient of this is:

$$\nabla g(\pmb{X})=2(\pmb{X}-\pmb{X}_0)+\lambda\sum_{i=1}^{L}\mathbb{I}\{g_j(\pmb{P}_i\pmb{X})-g_t(\pmb{P}_i\pmb{X})>0\}\left[\pmb{P}_i\left(\nabla g_j(\pmb{P}_i\pmb{X})-\nabla g_t(\pmb{P}_i\pmb{X})\right)\right]$$

We can still use the gradeint function defined previously and following snippet performs the attack on overlapping patches.

def overlapping_CW_attack(img, lamb, alpha, W, w, w0, save_freq=10, target_idx=0, max_iter=300, min_change=0.01):
  '''
  img:        the input image array
  lamb:       the regularization constant
  alpha:      the step size for gradient descent
  W:          the Wj and Wt matrix
  w:          the wj and wt vector
  w0:         the w_0j and w_0t scalar
  save_freq:  save image every k iteration. 0 or negative numbers mean don't save any images
  target_idx: which class to attack
  max_iter:   maximum number of iterations
  min_change: minimum change needed to prevent saturation
  '''
  idx = 0; change = 99  # initialize variables

  # M and N for the dimension of the input image
  M = len(img); N = len(img[0])

  result = np.copy(img)     # for storing the attacked image

  while idx < max_iter and change > min_change:
    perturb = np.zeros((M, N))  # to keep track of the perturbation
    
    for i in range(M - 8 + 1):
      for j in range(N - 8 + 1):
        # grab the current patch and the starting patch for gradient computation
        z = result[i : i + 8, j : j + 8].flatten('F')
        z_0 = img[i : i + 8, j : j + 8].flatten('F')

        # calculate the gradient
        
        grad = gradient(z, z_0, lamb, W, w, w0, target_idx)

        # add the patch to the perturbation matrix
        perturb[i : i + 8, j : j + 8] -= alpha * np.reshape(grad, (8, 8), order='F')
    
    # update the loop control variables
    idx += 1
    change = np.linalg.norm(perturb)
    # add the perturbation to the image
    result = np.clip(result + perturb, 0.0, 1.0)

    # save the image if necessary
    if save_freq > 0 and idx % save_freq == 0:
      classify_result = classifier_overlap(result, W, w, w0)
      plt.imsave(f'overlap_{lamb}_{idx}_img.png', result * 255, cmap='gray')
      plt.imsave(f'overlap_{lamb}_{idx}_perturb.png', (result - img) * 255, cmap='gray')
      plt.imsave(f'overlap_{lamb}_{idx}_clasify.png', classify_result * 255, cmap='gray')
  
  print(f'Finished in {idx} iterations.')
  return result

Part 3.7 - Attack!

We can attack the image by simply calling the functions defined previously. In this example, I will perform non-overlapping attack for $\lambda=1,5,10$ and overlapping attack with $\lambda=0.5,1,5$ and both with $\alpha=0.0001$.

if __name__ == '__main__':
  img_raw = plt.imread('data/cat_grass.jpg') / 255.0  # load the raw image and scale it to [0,1]
  img_truth = np.round(plt.imread('data/truth.png'))  # load the ground truth image and round them to 0 or 1
  W, w, w0 = load_data_and_compute()

  nonoverlapping_CW_attack(img_raw, 1, 0.0001, W, w, w0, save_freq=30, target_idx=0, max_iter=300, min_change=0.001)
  nonoverlapping_CW_attack(img_raw, 5, 0.0001, W, w, w0, save_freq=8, target_idx=0, max_iter=300, min_change=0.001)
  nonoverlapping_CW_attack(img_raw, 10, 0.0001, W, w, w0, save_freq=4, target_idx=0, max_iter=300, min_change=0.001)

  overlapping_CW_attack(img_raw, 0.5, 0.0001, W, w, w0, save_freq=10, target_idx=0, max_iter=300, min_change=0.01)
  overlapping_CW_attack(img_raw, 1, 0.0001, W, w, w0, save_freq=7, target_idx=0, max_iter=300, min_change=0.01)
  overlapping_CW_attack(img_raw, 5, 0.0001, W, w, w0, save_freq=2, target_idx=0, max_iter=300, min_change=0.01)

Part 4 - Results

Part 4.1 - Non-overlapping Attack Results

For non-overlapping attacks, following couple images shows the attack results.

For $\lambda=1$

Fig.3 - After 30 iterations.

Fig.4 - After 60 iterations.

Fig.5 - After 90 iterations.

For $\lambda=5$

Fig.6 - After 8 iterations.

Fig.7 - After 16 iterations.

Fig.8 - After 24 iterations.

For $\lambda=10$

Fig.9 - After 4 iterations.

Fig.10 - After 8 iterations.

Fig.11 - After 12 iterations.

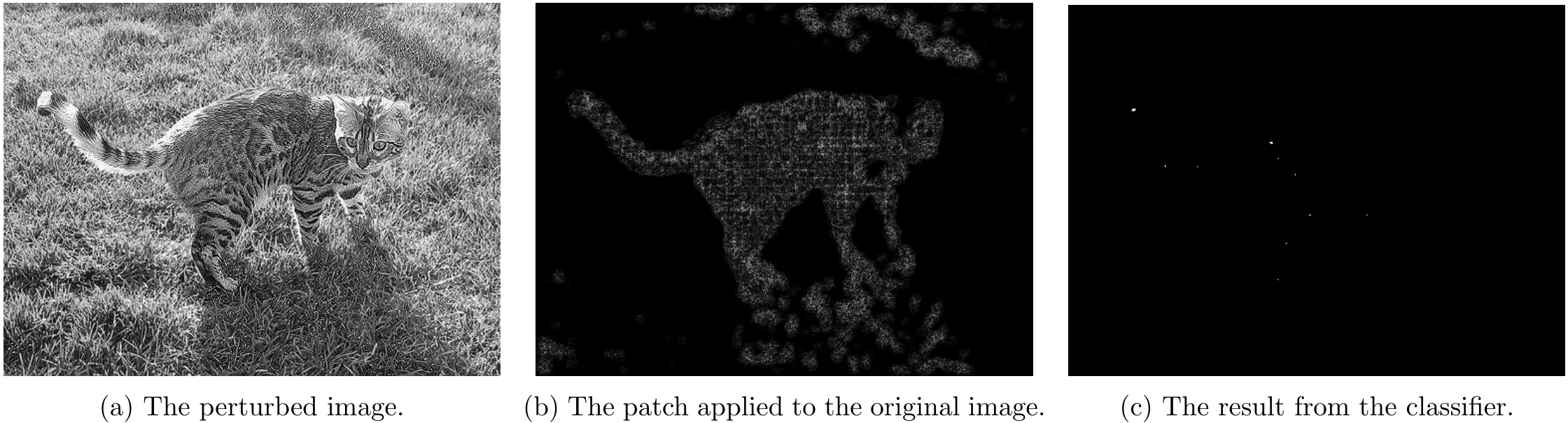
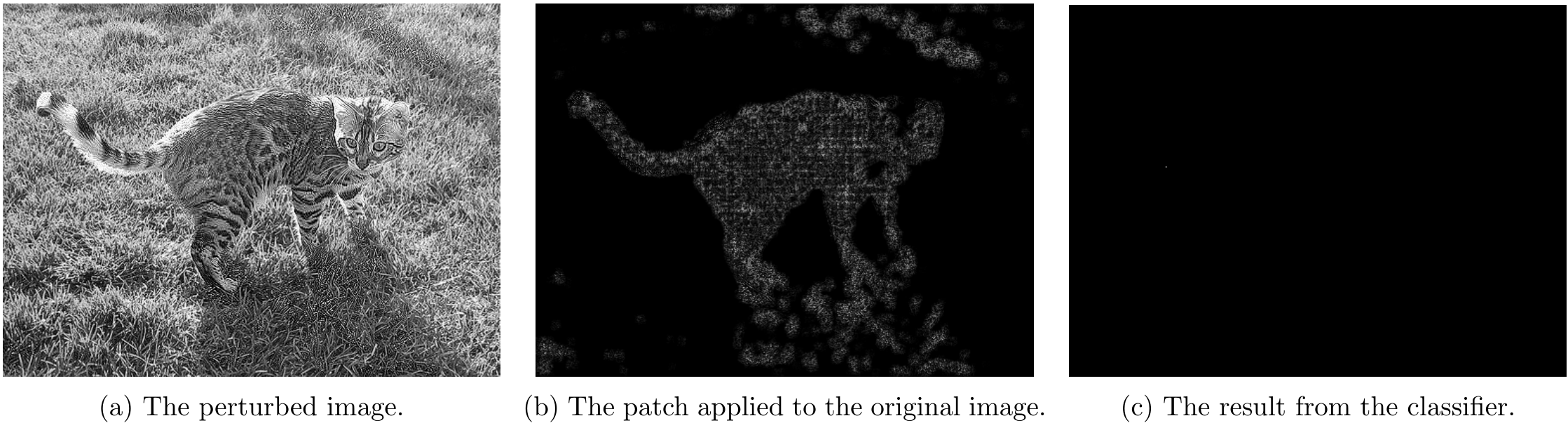
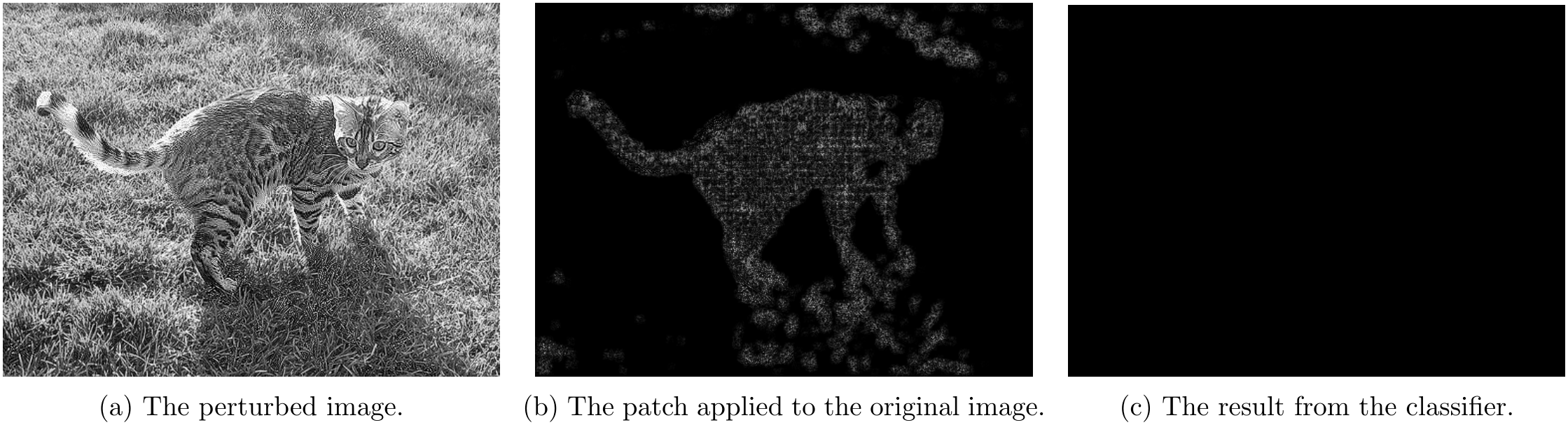
Part 4.2 - Overlapping Attack Results

For overlapping attacks, following couple images shows the attack results.

For $\lambda=0.5$

Fig.12 - After 10 iterations.

Fig.13 - After 20 iterations.

Fig.14 - After 29 iterations.

For $\lambda=1$

Fig.15 - After 7 iterations.

Fig.16 - After 14 iterations.

Fig.17 - After 21 iterations.

For $\lambda=5$

Fig.18 - After 2 iterations.

Fig.19 - After 4 iterations.

Fig.20 - After 6 iterations.

Appendix

1 - 2 Class Linear Classifier Minimum-Norm Attack

In case of two class linear classifier and minimizing the $l_2$ norm, the most optimal attack can be easily computed. In this case, the linear decision boundary between two classes can be defined as: $\pmb{w}^T\pmb{x}+w_0=0$ and solving the above constrained optimization is same as solveing for:

$$\min_{\pmb{x}}\|\pmb{x}-\pmb{x}_0\|^2\\\text{subject to\ \ \ }\pmb{w}^T\pmb{x}+w_0=0$$

The Lagrangian is defined as

$$\mathcal{L}(\pmb{x}, \lambda)=\frac{1}{2}\|\pmb{x}-\pmb{x}_0\|^2+\lambda\left(\pmb{w}^T\pmb{x}+w_0\right)$$

We can take the derivative with respect to both variable and set them to 0:

$$\begin{aligned}\nabla_{\pmb{x}}\mathcal{L}(\pmb{x}, \lambda)&=\pmb{x}-\pmb{x}_0+\lambda\pmb{w}=0\\\nabla_{\lambda}\mathcal{L}(\pmb{x}, \lambda)&=\pmb{w}^T\pmb{x}+w_0=0\end{aligned}$$

We can multiply the first equation by $\pmb{w}^T$ and sub-in the second equation to solve for $\lambda$:

$$\begin{aligned}0&=\pmb{w}^T\left(\pmb{x}-\pmb{x}_0\right)+\lambda\pmb{w}^T\pmb{w}\\0&=-w_0-\pmb{w}^T\pmb{x}_0+\lambda\|\pmb{w}\|_2\\\lambda^*&=\frac{\pmb{w}^T\pmb{x}_0+w_0}{\|\pmb{w}\|^2}\end{aligned}$$

Now we can sub $\lambda$ back into the first order optimality (the derivative of Lagrangian with respect to $\pmb{x}$) to solve for $\pmb{x}$:

$$\begin{aligned}\pmb{x}&=\pmb{x}_0-\lambda^*\pmb{w}\\\pmb{x}&=\pmb{x}_0-\left(\frac{\pmb{w}^T\pmb{x}_0+w_0}{\|\pmb{w}\|^2}\right)\pmb{w}\end{aligned}$$

This can be viewed as $\pmb{x}$ is a projection of $\pmb{x}_0$ on to the decision boundary along the direction of the gradient.

Fig.k - The visualization of the minimum-norm attack on 2 class linear classifier with l_2 norm.

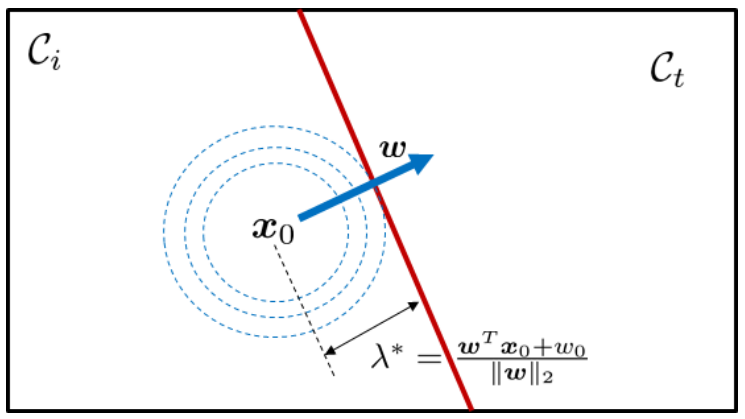
The solution to the $l_{\infty}$ norm

$$\begin{aligned}&\min_{\pmb{x}}\|\pmb{x}-\pmb{x}^{(k)}\|_{\infty}\\&\text{subject to\ \ }\pmb{w}^T\pmb{x}+w_0=0\end{aligned}$$

is given by

$$\pmb{x}=\pmb{x}_0-\left(\frac{\pmb{w}^T\pmb{x}_0+w_0}{\|\pmb{w}\|_1}\right)\cdot\text{sign}(\pmb{w}).$$

The detailed derivation can be found in Prof. Stanley Chan’s lecture notes.

2 - DeepFool Attack Iterative Approach

Given that $g(\pmb{x})$ is a nonlinear function, we can use iterative approach to approximate it using the gradient (or the first order derivative):

$$g(\pmb{x})\approx g\left(\pmb{x}^{(k)}\right)+\nabla_{\pmb{x}}g\left(\pmb{x}^{(k)}\right)^T\left(\pmb{x}-\pmb{x}^{(k)}\right)$$

Now the iterative problem becomes:

$$\begin{aligned}\pmb{x}^{(k+1)}=&\text{arg}\min_{\pmb{x}}\|\pmb{x}-\pmb{x}^{(k)}\|^2\\&\text{subject to\ \ }g\left(\pmb{x}^{(k)}\right)+\nabla_{\pmb{x}}g\left(\pmb{x}^{(k)}\right)^T\left(\pmb{x}-\pmb{x}^{(k)}\right)=0\end{aligned}$$

The equation is equivalent to solving linear classifier as shown in Appendix 1 where $\pmb{w}^{(k)}=\nabla_{\pmb{x}}g\left(\pmb{x}^{(k)}\right)$ and $w_{0}^{(k)}=g\left(\pmb{x}^{(k)}\right)-\nabla_{\pmb{x}}g\left(\pmb{x}^{(k)}\right)^T\pmb{x}^{(k)}$. The solution for the iterative process is:

$$\pmb{x}^{(k+1)}=\pmb{x}^{(k)}-\left(\frac{g\left(\pmb{x}^{(k)}\right)}{\|\nabla_{\pmb{x}}g\left(\pmb{x}^{(k)}\right)\|^2}\right)\nabla_{\pmb{x}}g\left(\pmb{x}^{(k)}\right)$$

where $\pmb{x}^{(0)}=\pmb{x}_0$.

3 - 2 Class Linear Classifier Maximum Allowable Attack

For two class situation where the decision boundary is $\pmb{w}^T\pmb{x}+w_0=0$, the optimization problem is:

$$\min_{\pmb{x}}\pmb{w}^T\pmb{x}+w_0\ \ \ \text{subject to}\ \ \|\pmb{x}-\pmb{x}_0\|\leq\eta$$

Let’s define $\pmb{x}=\pmb{x}_0+\pmb{r}$ where $\pmb{r}$ is the perturbation, then:

$$\begin{aligned}\pmb{w}^T\pmb{x}+w_0&=\pmb{w}^T\left(\pmb{x}_0+\pmb{r}\right)\\&=\pmb{w}^T\pmb{r}+\left(\pmb{w}^T\pmb{x}_0+w_0\right)\end{aligned}$$

Then define $b_0=\pmb{w}^T\pmb{x}_0+w_0$, the problem become:

$$\min_{\pmb{x}}\pmb{w}^T\pmb{r}+b_0\ \ \ \text{subject to}\ \ \ \|\pmb{r}\|\leq\eta.$$

$l_2$ Norm Example

For $L_2$ norm, we can solve the problem by first applying the Cauchy–Schwarz inequality:

$$\pmb{w}^T\pmb{r}\geq-\|\pmb{w}\|_2\|\pmb{r}\|_2\geq-\eta\|\pmb{w}\|_2$$

and we can claim that the lower bound of $\pmb{w}^T\pmb{r}$ is attained when $\pmb{r}=-\eta\pmb{w}/\|\pmb{w}\|_2$:

$$\begin{aligned}\pmb{w}^T\pmb{r}&=\pmb{w}^T\left(-\frac{\eta\pmb{w}}{\|\pmb{w}\|_2}\right)\\&=-\eta\|\pmb{w}\|_2\end{aligned}$$

Therefore the solution is:

$$\begin{aligned}\pmb{r}&=-\eta\frac{\pmb{w}}{\|\pmb{w}\|_2}\\\pmb{x}&=\pmb{x}_0-\eta\frac{\pmb{w}}{\|\pmb{w}\|_2}\end{aligned}$$

$l_{\infty}$ Norm Example

For $l_{\infty}$ norm, we can use the negative side of the Holder’s inequality and get:

$$\pmb{w}^T\pmb{r}\geq-\|\pmb{w}\|_1\|\pmb{r}\|_{\infty}\geq-\eta\|\pmb{w}\|_1.$$

We can also claim that the lower bound of $\pmb{w}^T\pmb{r}$ is attained when $\pmb{r}=-\eta\cdot\text{sign}\left(\pmb{w}\right)$:

$$\begin{aligned}\pmb{w}^T\pmb{r}&=-\eta\pmb{w}^T\text{sign}(\pmb{w})\\&=-\eta\sum_{i=1}^{d}w_i\text{sign}(w_i)\\&=-\eta\|\pmb{w}\|_1\end{aligned}$$

Therefore the solution is:

$$\begin{aligned}\pmb{r}&=-\eta\cdot\text{sign}\left(\pmb{w}\right)\\\pmb{x}&=\pmb{x}_0-\eta\cdot\text{sign}\left(\pmb{w}\right)\end{aligned}$$

4 - FGSM and i-FGSM

Again using the first order approximation, we can approximate $J(\pmb{x};\pmb{w})$ as:

$$\begin{aligned}J(\pmb{x};\pmb{w})&=J(\pmb{x}_0+\pmb{r};\pmb{w})\\&\approx J(\pmb{x}_0;\pmb{w})+\nabla_{\pmb{x}}J(\pmb{x}_0;\pmb{w})^T\pmb{r}\end{aligned}$$

We are trying to solve

$$\max_{\pmb{r}}J(\pmb{x}_0;\pmb{w})+\nabla_{\pmb{x}}J(\pmb{x}_0;\pmb{w})^T\pmb{r}\ \ \ \text{subject to }\ \ \|\pmb{r}\|\leq\eta$$

which is equivalent to solving

$$\min_{\pmb{r}}-\nabla_{\pmb{x}}J(\pmb{x}_0;\pmb{w})^T\pmb{r}-J(\pmb{x}_0;\pmb{w})\ \ \ \text{subject to }\ \ \|\pmb{r}\|\leq\eta.$$

By taking $\pmb{w}=-\nabla_{\pmb{x}}J(\pmb{x}_0;\pmb{w})$ and $w_0=-J(\pmb{x}_0;\pmb{w})$, the problem become same as what defined in Appendix 3. Therefore, the solution to the FGSM using $l_{\infty}$ norm is

$$\pmb{x}=\pmb{x}_0+\eta\cdot\text{sign}\left(\nabla_{\pmb{x}}J(\pmb{x}_0;\pmb{w})\right)$$

and for $l_2$ norm is

$$\pmb{x}=\pmb{x}_0+\eta\cdot\frac{\nabla_{\pmb{x}}J(\pmb{x}_0;\pmb{w})}{\|\nabla_{\pmb{x}}J(\pmb{x}_0;\pmb{w})\|_2}.$$

For iterative approach, we can use the similar first order approximation for $J$ as

$$\begin{aligned}J(\pmb{x};\pmb{w})&\approx J(\pmb{x}_0;\pmb{w})+\nabla_{\pmb{x}}J(\pmb{x}_0;\pmb{w})^T\pmb{r}\\&=J(\pmb{x}_0;\pmb{w})+\nabla_{\pmb{x}}J(\pmb{x}_0;\pmb{w})^T\pmb{x}-\nabla_{\pmb{x}}J(\pmb{x}_0;\pmb{w})^T\pmb{x}_0\end{aligned}$$

and the optimization problem become

$$\max_{\pmb{x}}J(\pmb{x}_0;\pmb{w})+\nabla_{\pmb{x}}J(\pmb{x}_0;\pmb{w})^T\pmb{x}-\nabla_{\pmb{x}}J(\pmb{x}_0;\pmb{w})^T\pmb{x}_0\ \ \ \text{subject to }\ \ \|\pmb{r}\|\leq\eta.$$

Since both the first term and the last term does not depends on $\pmb{x}$, we are safe to remove them from the equation. We can also add a bound to $\pmb{x}$ to between 0 and 1 to make sure the value does not explode. The iterative optimization problem is:

$$\begin{aligned}\pmb{x}^{(k+1)}=&\text{arg}\max_{\pmb{x}}\nabla_{\pmb{x}}J(\pmb{x}^{(k)};\pmb{w})^T\pmb{x}\\&\text{subject to }\ \|\pmb{x}-\pmb{x}^{(k)}\|\leq\eta,\ 0\leq\pmb{x}\leq1\end{aligned}$$

The solution for $l_{\infty}$ norm is

$$\pmb{x}^{(k+1)}=\mathcal{P}_{[0,1]}\left\{\pmb{x}^{(k)}+\eta\cdot\text{sign}\left(\nabla_{\pmb{x}}J(\pmb{x}^{(k)};\pmb{w})\right)\right\}$$

and for $l_2$ norm is

$$\pmb{x}^{(k+1)}=\mathcal{P}_{[0,1]}\left\{\pmb{x}^{(k)}+\eta\cdot\frac{\nabla_{\pmb{x}}J(\pmb{x}^{(k)};\pmb{w})}{\|\nabla_{\pmb{x}}J(\pmb{x}^{(k)};\pmb{w})\|_2}\right\}$$

5 - Source Code

import numpy as np
import matplotlib.pyplot as plt

def compute_variables(training_data, pi):
  mu = np.mean(training_data, 1)
  W = np.linalg.inv(np.cov(training_data))
  w = -np.matmul(W, mu)
  w0 = np.matmul(np.matmul(mu, W), mu) / 2 + np.log(np.linalg.det(np.cov(training_data))) / 2 - np.log(pi)

  return W, w, w0

def load_data_and_compute():
  train_grass = np.loadtxt('data/train_grass.txt', delimiter=',')
  train_cat = np.loadtxt('data/train_cat.txt', delimiter=',')
  W = [0] * 2
  w = [0] * 2
  w0 = [0] * 2
  W[0], w[0], w0[0] = compute_variables(train_grass, len(train_grass[0]) / (len(train_grass[0]) + len(train_cat[0])))
  W[1], w[1], w0[1] = compute_variables(train_cat, len(train_cat[0]) / (len(train_grass[0]) + len(train_cat[0])))

  return W, w, w0

def classifier_nonoverlap(img, W, w, w0):
  # find the dimension of the image
  M = len(img)
  N = len(img[0])

  output = np.zeros((M // 8 * 8, N // 8 * 8))   # initialize the output matrix
  for i in range(M // 8):
    for j in range(N // 8):
      # extract the 8x8 patch, flatten it and find the difference to the mu of cat and grass
      z = img[i * 8: i * 8 + 8, j * 8 : j * 8 + 8]
      z = z.flatten('F')

      # calculate g(x) and classify the batch based on sign(g(x))
      g = np.matmul(np.matmul(z.T, W[0] - W[1]), z) / 2 + np.matmul(z.T, w[0] - w[1]) + w0[0] - w0[1]
      if g > 0:
        output[i * 8 : i * 8 + 8, j * 8 : j * 8 + 8] = 1
  return output

def classifier_overlap(img, W, w, w0):
  # find the dimension of the image
  M = len(img)
  N = len(img[0])

  output = np.zeros((M - 8 + 1, N - 8 + 1))   # initialize the output matrix
  for i in range(M - 8 + 1):
    for j in range(N - 8 + 1):
      # extract the 8x8 patch, flatten it and find the difference to the mu of cat and grass
      z = img[i : i + 8, j : j + 8]
      z = z.flatten('F')

      # calculate g(x) and classify the pixel based on sign(g(x))
      g = np.matmul(np.matmul(z.T, W[0] - W[1]), z) / 2 + np.matmul(z.T, w[0] - w[1]) + w0[0] - w0[1]
      if g > 0:
        output[i][j] = 1
  return output

def gradient(z, z_0, lamb, W, w, w0, target_idx=0):
  '''
  z: 	   the current patch vector      x0: the original patch vector
  lamb:  lambda value                  W:  the Wj and Wt matrix
  w:     the wj and wt vector          w0: the w_0j and w_0t scalar
  target idx = 0 --> make cat into grass
  target idx = 1 --> make grass into cat
  '''
  j = 1 - target_idx
  t = target_idx
  # caluclate g(x) see if it is already in target class
  g = np.matmul(np.matmul(z.T, W[j] - W[t]), z) / 2 + np.matmul(z.T, w[j] - w[t]) + w0[j] - w0[t]
  if g > 0:
      return [0] * 64
  # if it is not in target class, calculate the gradient and return it
  grad = -2 * (z - z_0) - lamb * np.matmul(W[j] - W[t], z) + w[j] - w[t]
  return grad

def nonoverlapping_CW_attack(img, lamb, alpha, W, w, w0, save_freq=10, target_idx=0, max_iter=300, min_change=0.001):
  '''
  img:        the input image array
  lamb:       the regularization constant
  alpha:      the step size for gradient descent
  W:          the Wj and Wt matrix
  w:          the wj and wt vector
  w0:         the w_0j and w_0t scalar
  save_freq:  save image every k iteration. 0 or negative numbers mean don't save any images
  target_idx: which class to attack
  max_iter:   maximum number of iterations
  min_change: minimum change needed to prevent saturation
  '''
  idx = 0; change = 99  # initialize variables
  print(min_change)
  # M and N for the dimension of the input image
  M = len(img); N = len(img[0])

  result = np.copy(img)     # for storing the attacked image
  perturb = np.zeros((M, N))  # to keep track of the perturbation

  while idx < max_iter and change > min_change:
    for i in range(M // 8):
      for j in range(N // 8):
        # grab the current patch and the starting patch for gradient computation
        z = result[i * 8 : i * 8 + 8, j * 8 : j * 8 + 8].flatten('F')
        z_0 = img[i * 8 : i * 8 + 8, j * 8 : j * 8 + 8].flatten('F')

        # calculate the gradient
        grad = gradient(z, z_0, lamb, W, w, w0, target_idx)
        
        # add the patch to the perturbation matrix
        perturb[i * 8 : i * 8 + 8, j * 8 : j * 8 + 8] = -alpha * np.reshape(grad, (8, 8), order='F')
    
    # update the loop control variables
    idx += 1
    change = np.linalg.norm(perturb)
    print(idx, change)
    # add the perturbation to the image
    result = np.clip(result + perturb, 0.0, 1.0)

    # save the image if necessary
    if save_freq > 0 and idx % save_freq == 0:
      classify_result = classifier_nonoverlap(result, W, w, w0)
      plt.imsave(f'nonoverlap_{lamb}_{idx}_img.png', result * 255, cmap='gray')
      plt.imsave(f'nonoverlap_{lamb}_{idx}_perturb.png', (result - img) * 255, cmap='gray')
      plt.imsave(f'nonoverlap_{lamb}_{idx}_clasify.png', classify_result * 255, cmap='gray')
  
  print(f'Finished in {idx} iterations.')
  return result


def overlapping_CW_attack(img, lamb, alpha, W, w, w0, save_freq=10, target_idx=0, max_iter=300, min_change=0.01):
  '''
  img:        the input image array
  lamb:       the regularization constant
  alpha:      the step size for gradient descent
  W:          the Wj and Wt matrix
  w:          the wj and wt vector
  w0:         the w_0j and w_0t scalar
  save_freq:  save image every k iteration. 0 or negative numbers mean don't save any images
  target_idx: which class to attack
  max_iter:   maximum number of iterations
  min_change: minimum change needed to prevent saturation
  '''
  idx = 0; change = 99  # initialize variables

  # M and N for the dimension of the input image
  M = len(img); N = len(img[0])

  result = np.copy(img)     # for storing the attacked image

  while idx < max_iter and change > min_change:
    perturb = np.zeros((M, N))  # to keep track of the perturbation
    
    for i in range(M - 8 + 1):
      for j in range(N - 8 + 1):
        # grab the current patch and the starting patch for gradient computation
        z = result[i : i + 8, j : j + 8].flatten('F')
        z_0 = img[i : i + 8, j : j + 8].flatten('F')

        # calculate the gradient
        
        grad = gradient(z, z_0, lamb, W, w, w0, target_idx)

        # add the patch to the perturbation matrix
        perturb[i : i + 8, j : j + 8] -= alpha * np.reshape(grad, (8, 8), order='F')
    
    # update the loop control variables
    idx += 1
    change = np.linalg.norm(perturb)
    # add the perturbation to the image
    result = np.clip(result + perturb, 0.0, 1.0)

    # save the image if necessary
    if save_freq > 0 and idx % save_freq == 0:
      classify_result = classifier_overlap(result, W, w, w0)
      plt.imsave(f'overlap_{lamb}_{idx}_img.png', result * 255, cmap='gray')
      plt.imsave(f'overlap_{lamb}_{idx}_perturb.png', (result - img) * 255, cmap='gray')
      plt.imsave(f'overlap_{lamb}_{idx}_clasify.png', classify_result * 255, cmap='gray')
  
  print(f'Finished in {idx} iterations.')
  return result

if __name__ == '__main__':
  img_raw = plt.imread('data/cat_grass.jpg') / 255.0  # load the raw image and scale it to [0,1]
  img_truth = np.round(plt.imread('data/truth.png'))  # load the ground truth image and round them to 0 or 1
  W, w, w0 = load_data_and_compute()

  nonoverlapping_CW_attack(img_raw, 1, 0.0001, W, w, w0, save_freq=30, target_idx=0, max_iter=300, min_change=0.001)
  nonoverlapping_CW_attack(img_raw, 5, 0.0001, W, w, w0, save_freq=8, target_idx=0, max_iter=300, min_change=0.001)
  nonoverlapping_CW_attack(img_raw, 10, 0.0001, W, w, w0, save_freq=4, target_idx=0, max_iter=300, min_change=0.001)

  overlapping_CW_attack(img_raw, 0.5, 0.0001, W, w, w0, save_freq=10, target_idx=0, max_iter=300, min_change=0.01)
  overlapping_CW_attack(img_raw, 1, 0.0001, W, w, w0, save_freq=7, target_idx=0, max_iter=300, min_change=0.01)
  overlapping_CW_attack(img_raw, 5, 0.0001, W, w, w0, save_freq=2, target_idx=0, max_iter=300, min_change=0.01)